Statistics Homework Guide

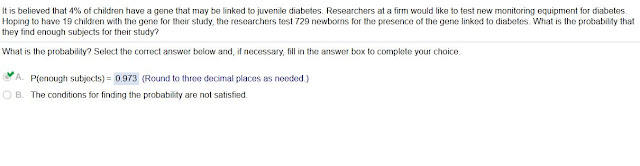
Question 

It is believed that 4​% of children have a gene that may be linked to juvenile diabetes. Researchers at a firm would like to test new monitoring equipment for diabetes. Hoping to have 19 children with the gene for their​ study, the researchers test 729 newborns for the presence of the gene linked to diabetes. What is the probability that they find enough subjects for their​ study?

Begin by checking that the randomization​ condition, 10%​ condition, and​ success/failure condition are all satisfied.

To satisfy the randomization​ condition, the sampling method must not be biased and the data must be representative of the population. This condition is satisfied because the sample of newborns is a random sample of the population of newborns.

To satisfy the​ 10% condition, the sample​ size, n, must be no larger than​ 10% of the population. This condition is satisfied because it is safe to assume that there are more than

7100 newborns available to be randomly tested.

To satisfy the​ success/failure condition, the sample size must be big enough so that both the number of​ "successes," np, and the number of​ "failures," nq, are expected to be at least 10. 

np = 28.4 and nq = 681.6

Since both np and nq are greater than​ 10, the​ success/failure condition is satisfied.

Since the conditions are​ satisfied, use a normal model for the sampling distribution of phat .Remember that the researchers are hoping to obtain at least 18 children for the experiment. To find the value that phat must be greater than or equal to for the researchers to find enough​ subjects, divide the number of desired subjects by the sample size.

phat = 18/710 = 0.0254

This means that the objective is to find P where (phat >0.0254)

mean of phat = 0.04 and the standard deviation is (√(0.04*0.96/710) = 0.0074

 So Z = (0.0254-0.04)/0.0074 = -1.97

Therefore using a standard normal table,  P(phat > 0.0254) = P(Z>-1.97) = 0.976